Урок «Двугранный угол.

«Двугранный угол» - Найдите расстояние от точки В до плоскости. Угол С острый. Треугольник АВС – тупоугольный. Угол С тупой. Расстояние от точки до прямой. В тетраэдре DАВС все ребра равны. Угол между наклонными. Расстояние между основаниями наклонных. Линейные углы двугранного угла равны. Алгоритм построения линейного угла.

«Двугранный угол геометрия» - угол РСВ - линейный для двугранного угла с ребром АС. Найти (увидеть) ребро и грани двугранного угла. Модель может быть как объемной, так и складной. Сечение двугранного угла плоскостью, перпендикулярной ребру. Грани. прямая СР перпендикулярна ребру СА (по теореме о трех перпендикулярах). угол РКВ - линейный для двугранного угла с РСАВ.

«Трёхгранный угол» - Признаки равенства трехгранных углов. Дано: Оabc – трехгранный угол; ?(b; c) = ?; ?(a; c) = ?; ?(a; b) = ?. Урок 6. Следствия. 1) Для вычисления угла между прямой и плоскостью применима формула: Формула трех косинусов. . Дан трехгранный угол Оabc. Трехгранный угол. Теорема. В правильной треугольной пирамиде плоский угол при вершине меньше 120?.

«Трёхгранные и многогранные углы» - Трехгранные углы додекаэдра. Трехгранные и четырехгранные углы ромбододекаэдра. Четырехгранные углы октаэдра. Трехгранные углы тетраэдра. Измерение многогранных углов. Задача. Многогранные углы. Пятигранные углы икосаэдра. Вертикальные многогранные углы. Трехгранный угол пирамиды. Пусть SA1…An – выпуклый n-гранный угол.

«Угол между прямой и плоскостью» - В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AC1 и плоскостью ADE1. В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AA1 и плоскостью ACE1. Угол между прямой и плоскостью. В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямой AB1 и плоскостью ADE1.

«Многогранный угол» - Выпуклые многогранные углы. Многогранные углы. В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д. В) икосаэдр. Два плоских угла трехгранного угла равны 70° и 80°. Следовательно, ? ASB + ? BSC + ? ASC < 360° . Сумма плоских углов трехгранного угла меньше 360°.

Всего в теме 9 презентаций

Понятие двугранного угла

Для введения понятия двугранного угла, для начала вспомним одну из аксиом стереометрии.

Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях -- по разные стороны от прямой $a$ (рис. 1).

Рисунок 1.

На этой аксиоме основан принцип построение двугранного угла.

Определение 1

Фигура называется двугранным углом , если она состоит из прямой и двух полуплоскостей этой прямой, не принадлежащих одной плоскости.

При этом полуплоскости двугранного угла называются гранями , а прямая, разделяющая полуплоскости -- ребром двугранного угла (рис. 1).

Рисунок 2. Двугранный угол

Градусная мера двугранного угла

Определение 2

Выберем на ребре произвольную точку $A$. Угол между двумя прямыми, лежащими в разных полуплоскостях, перпендикулярных ребру и пересекающихся в точке $A$ называется линейным углом двугранного угла (рис. 3).

Рисунок 3.

Очевидно, что каждый двугранный угол имеет бесконечное число линейных углов.

Теорема 1

Все линейные углы одного двугранного угла равняются между собой.

Доказательство.

Рассмотрим два линейных угла $AOB$ и $A_1{OB}_1$ (рис. 4).

Рисунок 4.

Так как лучи $OA$ и ${OA}_1$ лежат в одной полуплоскости $\alpha $ и перпендикулярны одной прямой, то они являются сонаправленными. Так как лучи $OB$ и ${OB}_1$ лежат в одной полуплоскости $\beta $ и перпендикулярны одной прямой, то они являются сонаправленными. Следовательно

\[\angle AOB=\angle A_1{OB}_1\]

В силу произвольности выборов линейных углов. Все линейные углы одного двугранного угла равны между собой.

Теорема доказана.

Определение 3

Градусной мерой двугранного угла называется градусная мера линейного угла двугранного угла.

Примеры задач

Пример 1

Пусть нам даны две неперпендикулярные плоскости $\alpha $ и $\beta $ которые пересекаются по прямой $m$. Точка $A$ принадлежит плоскости $\beta $. $AB$ -- перпендикуляр к прямой $m$. $AC$ перпендикуляр к плоскости $\alpha $ (точка $C$ принадлежит $\alpha $). Доказать, что угол $ABC$ является линейным углом двугранного угла.

Доказательство.

Изобразим рисунок по условию задачи (рис. 5).

Рисунок 5.

Для доказательства вспомним следующую теорему

Теорема 2: Прямая, проходящая через основание наклонной, перпендикулярно ей, перпендикулярна её проекции.

Так как $AC$ - перпендикуляр к плоскости $\alpha $, то точка $C$ - проекция точки $A$ на плоскость $\alpha $. Следовательно, $BC$ -- проекция наклонной $AB$. По теореме 2, $BC$ перпендикулярна ребру двугранного угла.

Тогда, угол $ABC$ удовлетворяет всем требованиям определения линейного угла двугранного угла.

Пример 2

Двугранный угол равен $30^\circ$. На одной из граней лежит точка $A$, которая удалена от другой грани на расстояние $4$ см. Найти расстояние от точки $A$ до ребра двугранного угла.

Решение.

Будем рассматривать рисунок 5.

По условию, имеем $AC=4\ см$.

По определению градусной меры двугранного угла, имеем, что угол $ABC$ равен $30^\circ$.

Треугольник $ABC$ является прямоугольным треугольником. По определению синуса острого угла

\[\frac{AC}{AB}=sin{30}^0\] \[\frac{5}{AB}=\frac{1}{2}\] \

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

В планиметрии основными объектами являются прямые, отрезки, лучи и точки. Лучи исходящие из одной точки, образуют одну их геометрических фигур-угол.

Мы знаем, что линейный угол измеряется в градусах и радианах.

В стереометрии к объектам добавляется плоскость. Фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости в геометрии называется двугранным углом. Полуплоскости - это грани двугранного угла. Прямая а - это ребро двугранного угла.

Двухгранный угол как и линейный угол можно назвать, измерить, построить. Это и предстоит нам выяснить в этом уроке.

Найдём двухгранный угол на модели тетраэдра АВСD.

Двугранный угол с ребром АВ называют CABD, где С и D точки принадлежащие разным граням угла а ребро АВ называют в середине

Вокруг нас достаточно много предметов с элементами в виде двухгранного угла.

Во многих городах в парках установлены специальные скамейки для примирения. Скамейка выполнена в виде двух сходящихся к центру наклонных плоскостей.

При строительстве домов часто используется так называемая двухскатная крыша. На этом доме крыша выполнена в виде двухгранного угла в 90 градусов.

Двугранный угол тоже измеряется в градусах или радианах, но как его измерить.

Интересно заметить, что крыши домов лежат на стропилах. А обрешётка стропил образует два ската крыши под заданным углом.

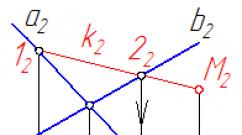
Перенесем изображение на чертёж. На чертеже для нахождения двухгранного угла на его ребре отмечается точка В. Из этой точки проводятся два луча ВА и ВС перпендикулярно ребру угла. Образованный этими лучами угол АВС называется линейным углом двугранного угла.

Градусная мера двугранного угла равна градусной мере его линейного угла.

Измерим угол АОВ.

Градусная мера данного двугранного угла равна шестидесяти градусам.

Линейных углов для двугранного угла можно провести бесконечное количество, важно знать, что все они равны.

Рассмотрим два линейных угла АОВ и А1О1В1 . Лучи ОА и О1А1 лежат в одной грани и перпендикулярны к прямой ОО1, поэтому они сонаправлены. Лучи ОВ и О1В1 так же сонаправлены. Поэтому угол АОВ равен углуА1О1В1 как углы с сонаправленными сторонами.

Так двугранный угол характеризуется линейным углом, а линейные углы бывают острые, тупые и прямые. Рассмотрим модели двугранных углов.

Тупой угол, если его линейный угол от 90 до 180 градусов.

Прямой угол, если его линейный угол равен 90 градусов.

Острый угол, елси его линейный угол от 0 до 90 градусов.

Докажем одно из важных свойств линейного угла.

Плоскость линейного угла перпендикулярна к ребру двугранного угла.

Пусть угол АОВ - линейный угол данного двугранного угла. По построению лучи АО и ОВ перпендикулярные прямой а.

Через две пересекающиеся прямые АО и ОВ проходит плоскость АОВ по теореме: Через две пересекающиеся прямые проходит плоскость и притом только одна.

Прямая а перпендикулярна двум пересекающимся прямым лежащим в этой плоскости, значит по признаку перпендикулярности прямой и плоскости прямая а перпендикулярна плоскости АОВ.

Для решения задач важно уметь строить линейный угол заданного двухгранного угла. Построить линейный угол двугранного угла с ребром АВ для тетраэдра АВСD.

Речь идет о двугранном угле, который образован, во-первых, ребром АВ, одной гранью АВD, второй гранью АВС.

Вот один из способов построения.

Проведем перпендикуляр из точки D к плоскости АВС, Отметим точку М основание перпендикуляра. Вспомним, что в тетраэдре основание перпендикуляра совпадает с центром вписанной окружности в основание тетраэдра.

Проведем наклонную из точки D перпендикулярно к ребру АВ, отметим точку N основание наклонной.

В треугольнике DMN отрезок NM будет проекций наклонной DN на плоскость АВС. По теореме о трёх перпендикулярах ребро АВ будет перпендикулярно проекции NМ.

Значит cтороны угла DNM перпендикулярны к ребру АВ, значит построенный угол DNM искомый линейный угол.

Рассмотрим пример решения задачи на вычисление двугранного угла.

Равнобедренный треугольник АВС и правильный треугольник АDB не лежат в одной плоскости. Отрезок CD является перпендикуляром к плоскости ADB. Найдите двугранный угол DABC, если AC=CB=2 см, АB= 4см.

Двугранный угол DABC равен его линейному углу. Построим этот угол.

Проведем наклонную СМ перпендикулярно к ребру АВ, так как треугольник АСВ равнобедренный, то точка М совпадёт с серединой ребра АВ.

Прямая СD по условию перпендикулярна плоскости ADB, значит перпендикулярна прямой DM лежащей в этой плоскости. А отрезок МD является проекцией наклонной СМ на плоскость АDВ.

Прямая АВ перпендикулярна наклонной СМ по построению, значит по теореме о трех перпендикулярах перпендикулярна проекции MD.

Итак к ребру АВ найдены два перпендикуляра СМ и DМ. Значит они образуют линейный угол СMD двугранного угла DАВС. И нам останется его найти из прямоугольного треугольника СDM.

Так отрезок СМ медиана и высота равнобедренного треугольника АСВ, то по теореме Пифагора катет СМ равен 4 см.

Из прямоугольного треугольника DMB по теореме Пифагора катет DM равен двум корням из трёх.

Косинус угла из прямоугольного треугольника равен отношению прилежащего катета МD к гипотенузе СМ и равен три корня из трёх на два. Значит угол СМD равен 30 градусам.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Величину угла между двумя различными плоскостями можно определить для любого взаимного расположения плоскостей.

Тривиальный случай если плоскости параллельны. Тогда угол между ними считается равным нулю.

Нетривиальный случай если плоскости пересекаются. Этому случаю и посвящено дальнейшее обсуждение. Сначала нам понадобится понятие двугранного угла.

9.1 Двугранный угол

Двугранный угол это две полуплоскости с общей прямой (которая называется ребром двугранного угла). На рис. 50 изображён двугранный угол, образованный полуплоскостями и; ребром этого двугранного угла служит прямая a, общая для данных полуплоскостей.

Рис. 50. Двугранный угол

Двугранный угол можно измерять в градусах или радианах словом, ввести угловую величину двугранного угла. Делается это следующим образом.

На ребре двугранного угла, образованного полуплоскостями и, возьмём произвольную точку M. Проведём лучи MA и MB, лежащие соответственно в данных полуплоскостях и перпендикулярные ребру (рис. 51 ).

Рис. 51. Линейный угол двугранного угла

Полученный угол AMB это линейный угол двугранного угла. Угол " = \AMB как раз и является угловой величиной нашего двугранного угла.

Определение. Угловая величина двугранного угла это величина линейного угла данного двугранного угла.

Все линейные углы двугранного угла равны друг другу (ведь они получаются друг из друга параллельным сдвигом). Поэтому данное определение корректно: величина " не зависит от конкретного выбора точки M на ребре двугранного угла.

9.2 Определение угла между плоскостями

При пересечении двух плоскостей получаются четыре двугранных угла. Если все они имеют одинаковую величину (по 90), то плоскости называются перпендикулярными; угол между плоскостями тогда равен 90 .

Если не все двугранные углы одинаковы (то есть имеются два острых и два тупых), то углом между плоскостями называется величина острого двугранного угла (рис. 52 ).

Рис. 52. Угол между плоскостями

9.3 Примеры решения задач

Разберём три задачи. Первая простая, вторая и третья примерно на уровне C2 на ЕГЭ по математике.

Задача 1. Найдите угол между двумя гранями правильного тетраэдра.

Решение. Пусть ABCD правильный тетраэдр. Проведём медианы AM и DM соответствующих граней, а также высоту тетраэдра DH (рис. 53 ).

Рис. 53. К задаче 1

Будучи медианами, AM и DM являются также высотами равносторонних треугольников ABC и DBC. Поэтому угол " = \AMD есть линейный угол двугранного угла, образованного гранями ABC и DBC. Находим его из треугольника DHM:

Ответ: arccos 1 3 .

Задача 2. В правильной четырёхугольной пирамиде SABCD (с вершиной S) боковое ребро равно стороне основания. Точка K середина ребра SA. Найдите угол между плоскостями

Решение. Прямая BC параллельна AD и тем самым параллельна плоскости ADS. Поэтому плоскость KBC пересекает плоскость ADS по прямой KL, параллельной BC (рис. 54 ).

Рис. 54. К задаче 2

При этом KL будет также параллельна прямой AD; следовательно, KL средняя линия треугольника ADS, и точка L середина DS.

Проведём высоту пирамиды SO. Пусть N середина DO. Тогда LN средняя линия треугольника DOS, и потому LN k SO. Значит, LN перпендикуляр к плоскости ABC.

Из точки N опустим перпендикуляр NM на прямую BC. Прямая NM будет проекцией наклонной LM на плоскость ABC. Из теоремы о трёх перпендикулярах следует тогда, что LM также перпендикулярна BC.

Таким образом, угол " = \LMN является линейным углом двугранного угла, образованного полуплоскостями KBC и ABC. Будем искать этот угол из прямоугольного треугольника LMN.

Пусть ребро пирамиды равно a. Сначала находим высоту пирамиды:

Решение. Пусть L точка пересечения прямых A1 K и AB. Тогда плоскость A1 KC пересекает плоскость ABC по прямой CL (рис.55 ).

A C

Рис. 55. К задаче 3

Треугольники A1 B1 K и KBL равны по катету и острому углу. Следовательно, равны и другие катеты: A1 B1 = BL.

Рассмотрим треугольник ACL. В нём BA = BC = BL. Угол CBL равен 120 ; стало быть, \BCL = 30 . Кроме того, \BCA = 60 . Поэтому \ACL = \BCA + \BCL = 90 .

Итак, LC ? AC. Но прямая AC служит проекцией прямой A1 C на плоскость ABC. По теореме о трёх перпендикулярах заключаем тогда, что LC ? A1 C.

Таким образом, угол A1 CA линейный угол двугранного угла, образованного полуплоскостями A1 KC и ABC. Это и есть искомый угол. Из равнобедренного прямоугольного треугольника A1 AC мы видим, что он равен 45 .